声明:本文来自于微信公众号 机器之心,作者:机器之心,授权站长之家转载发布。
蒸馏模型的性能可以量化估算了。
众所周知,知识蒸馏技术当前正被大模型领域广泛使用,它可以在大幅压缩模型体量的同时保持一定的性能、降低模型时延、提升模型精度,与此同时还能对知识域进行集成和迁移。
近日,苹果研究人员提出了一种蒸馏扩展定律(Distillation Scaling Laws),基于计算预算及其在学生和教师之间的分配,我们现在开始可以估算蒸馏模型的性能了。
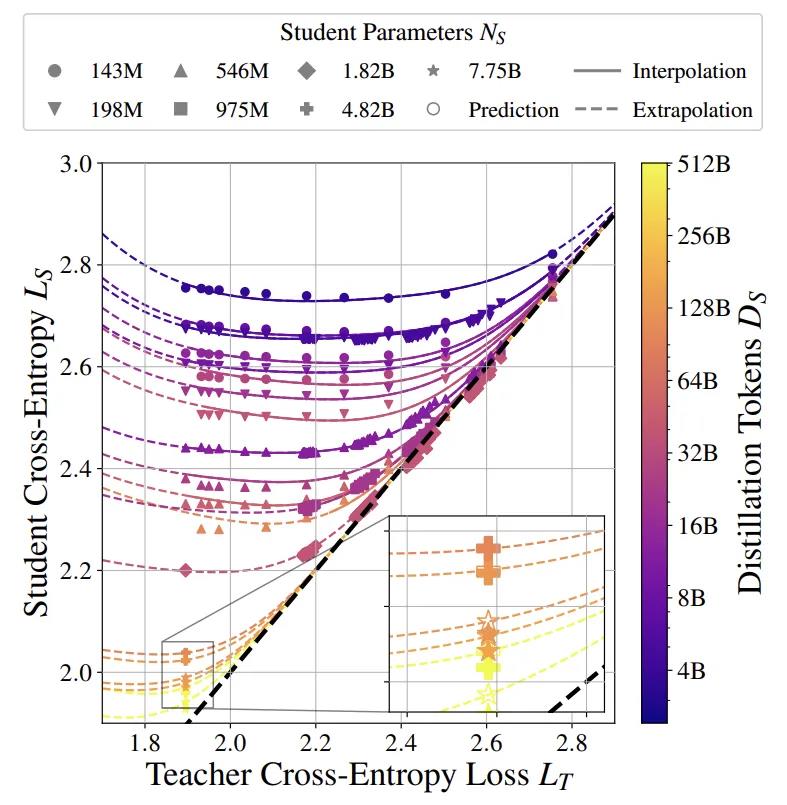
图1. 蒸馏扩展定律的外推。蒸馏扩展定律适用于一系列损失为 LT 的教师的弱学生模型(L_S >2.3)。实线表示给定学生配置(插值)下未见过的教师的预测模型行为,虚线表示见过的教师之外和强学生区域(L_S ≤2.3)的预测模型行为。如图所示,学生的表现可以胜过老师(详情见图2、3和41)。
苹果研究者认为,该发现降低了大规模使用蒸馏的风险,现在我们可以基于此优化教师和学生模型的计算分配,以最大化学生模型的性能。该工作提供的计算最优的蒸馏方案适用于两种情况:1)已有教师模型,或2)需要训练教师模型。
如果要蒸馏多个学生模型,或者已有教师模型,蒸馏在计算水平上优于监督预训练,直到计算水平随着学生模型规模的增加而可预测地增长。如果要蒸馏一个学生模型且还需要训练教师模型,则应采用监督学习。此外,作者在大规模蒸馏研究中提供了深入的见解,这些见解增加了我们对蒸馏的理解,并为实验设计提供了信息。

- 论文标题:Distillation Scaling Laws
- 论文链接:https://arxiv.org/pdf/2502.08606
大模型的扩展定律(Scaling Laws)表明,如果先前训练的语言模型(LM)遵循计算最优训练范式,就可以随着计算力提升而提升。由于推理成本的持续增长,目前这种定律难以持续,人们尝试使用过度训练(其中训练数据量远大于计算最优情况)来实现小型、功能强大的模型。这些模型的构建既昂贵又耗时。
我们正在寻求与训练算力投入相匹配,但训练成本更低的模型,蒸馏是一种流行的方法。但长期以来,学界对蒸馏缺乏共识,并不了解如何分配计算资源,以产生最强大的模型。为了弥补这一知识差距,研究人员对蒸馏进行了广泛研究,学生和老师的参数范围从1.43亿到126亿,使用训练数据最多达5120亿 token。
研究发现:

1. 一个大小为 N_S 的学生模型,通过从大小为 N_T 的教师模型中蒸馏 D_S 个 token 所得到的交叉熵,可以通过蒸馏扩展定律(公式8)进行预测。
2. 老师大小 N_T 和老师训练 token 数量 D_T 仅通过确定老师的交叉熵 L_T = L_T (N_T , D_T) 来确定学生交叉熵;
3. 老师交叉熵对学生损失的影响遵循幂律,该幂律根据学生和老师的相对学习能力在两种行为之间转换,反映了蒸馏中称为能力差距的现象,即较强的老师会产生较差的学生。该工作的参数化解决了有关能力差距悬而未决的问题,表明这是老师和学生之间学习能力(假设空间和优化能力)的差距,而不仅仅是他们的相对大小,后者其实是一种特殊情况。
该结果表明,当两个学习过程都有足够的数据或计算时,蒸馏不能产生比监督学习更低的模型交叉熵。但是,如果以下两个条件都成立,则蒸馏比监督学习更有效:
1. 用于学生的总计算或 token 不大于新扩展定律给出的学生大小相关阈值;
2. 老师已经存在,或者要训练的老师有超出单次蒸馏的用途。
新的定律和分析有望指导 AI 社区构建更强大的模型,实现更低的推理成本和总计算成本。
蒸馏扩展率
文章概述了他们如何得出蒸馏扩展率所采取的步骤。
首先是实验设置。本文的目标是理解教师模型在蒸馏过程中的作用,因此,该研究在纯蒸馏情况下(λ =1,公式7)进行蒸馏,以避免数据带来的混淆。本文验证了 λ =1的选择能够产生与最优 λ∗ 统计相似的结果。同样,所有实验均使用蒸馏温度(τ =1),因为该研究发现这能产生性能最佳的学生模型。

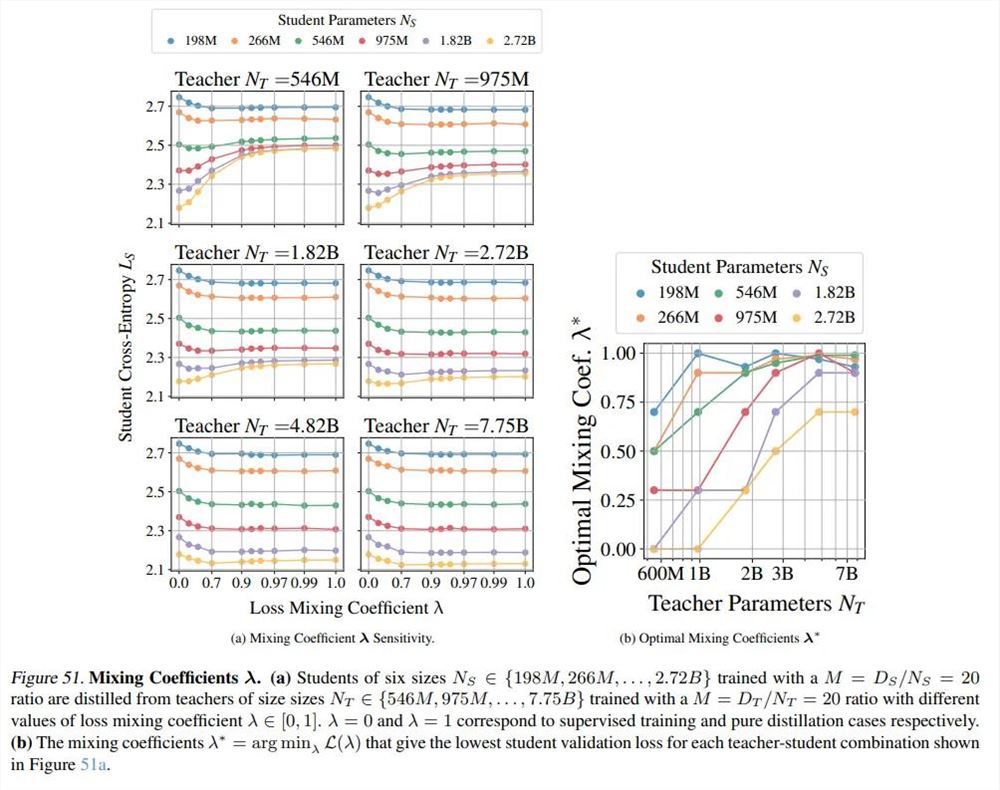
表1是文中出现的符号代表内容:


对应中文版本
此外,对于实验数据的选择,本文结合了三种方案:
固定 M 的教师 / 学生 IsoFLOP 实验:
本文预测在固定教师模型的情况下,学生模型的参数(N_S)和训练 token 数量(D_S)之间会呈现出幂律行为。
为了在给定的计算预算内生成尽可能多样的教师模型,本文训练了六个 Chinchilla 最优教师模型,其参数范围从1.98亿到77.5亿。对于每一个教师模型,本文按照标准训练成本,将其蒸馏到具有四种 IsoFLOP 配置的学生模型中。最终得到的学生模型交叉熵如图2所示。作者还注意到,在某些情况下,学生模型能够超越教师模型的表现,即展现出弱到强的泛化能力。

注:为实现扩展系数的可靠识别,此前有研究使用了两种策略:
- (固定模型,变化数据) 对于一个固定的模型族,变化训练 token 的数量。
- (IsoFLOP 配置) 在总计算约束下,同时变化模型大小和训练 token 的数量。
为了确保实验能够检测到这种影响,本文设定学生(N_S,D_S)是固定的,而 N_T 和 D_T 在计算约束下变化。本文进行了蒸馏实验,将四个 Chinchilla 最优(M_S = D_S/N_S ≈20)的学生(其参数范围从1.98亿到18.2亿),从根据四种 IsoFLOP 配置训练的教师中蒸馏出来。最终得到的学生交叉熵如图3所示。

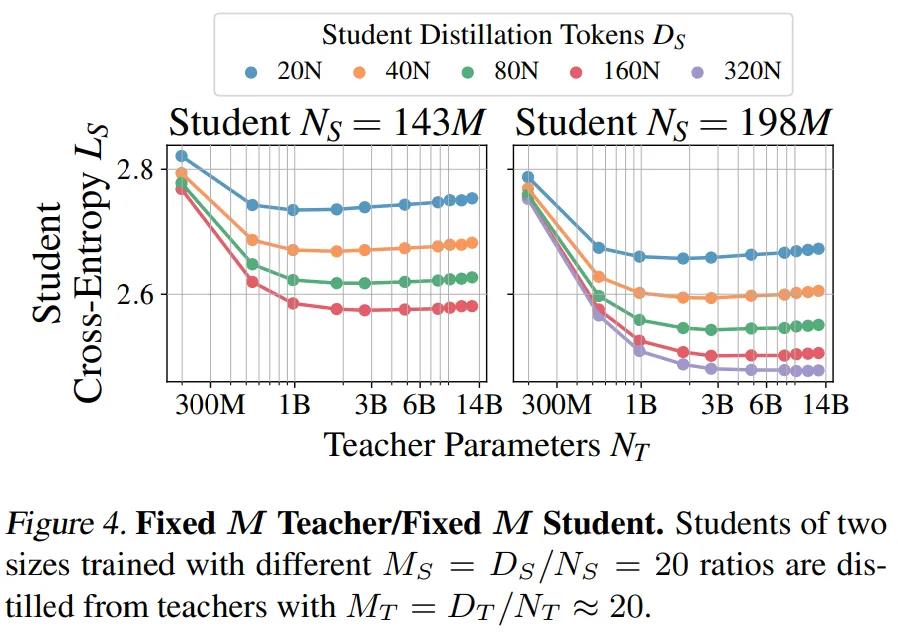
最后,本文训练了固定 M 的教师模型与固定 M 的学生模型的组合,其中包含十个教师模型(M_T ≈20)和五种规模的学生模型,每个学生模型至少对应四种 M_S 选择。其中两个学生模型的交叉熵结果如图4所示。
此外,本文还需要确定蒸馏扩展定律的函数形式。首先,本文观察到教师模型的大小 N_T 和预训练 token 数量 D_T 的贡献可以通过教师模型的交叉熵 L_T 来总结。这可以从图1和图3b 中看出:

总之,本文提出,学生交叉熵在 L_T 中遵循 broken 幂律,在 N_S 和 D_S 中遵循幂律:

在此之后,论文分析了在不同计算预算下如何最优地分配教师和学生模型的资源,包括教师模型的训练成本和学生模型的蒸馏成本,并比较了蒸馏和监督学习在不同计算预算下的性能,发现当教师模型的训练成本被考虑时,监督学习通常更有效。
这项工作代表了已知最大规模的蒸馏受控实证研究,系统消融了常见的蒸馏技术。正如监督扩展减轻了监督预训练中的风险一样,新工作为生产更小、更强大的模型提供了路线图,并增强了测试时扩展的可行性。
